Hace meses empezamos una nueva serie, Las cuatro fuerzas, en la que pretendemos desgranar las fuerzas fundamentales de la Naturaleza y hablar con cierta profundidad de cada una: qué la hace especial, cuándo fue descubierta, cómo ha ido evolucionando nuestro conocimiento sobre ella y qué cosas siguen sin encajar mirando hacia el futuro.

En los dos primeros artículos (primero y segundo) hablamos sobre el propio concepto de fuerza: nuestras ideas primitivas sobre ella y su florecimiento como concepto estrictamente científico bajo Isaac Newton. Sé que hace mucho tiempo, pero es que no doy abasto y hay muchas otras series que continuar y poco tiempo para escribir.

Hoy nos centraremos en la primera fuerza fundamental en ser identificada y descrita como tal, precisamente por Newton: la fuerza gravitatoria.

Si has leído la introducción a la serie –y si no lo has hecho, deberías antes de seguir leyendo este artículo– ya sabes que las primeras nociones científicas sobre la gravedad se las debemos a Aristóteles. Pero, como también te imaginarás, a pesar de su inteligencia el griego estaba profundamente equivocado en prácticamente todo.

Ya describimos la idea general en la introducción. De acuerdo con Aristóteles las sustancias tienen un lugar natural que les corresponde dependiendo de su gravedad o levedad. Las sustancias más graves, es decir, más pesadas, tienden a moverse hasta el centro del Universo, que es el centro de la Tierra, y de ahí que exista una esfera sólida alrededor de ese punto (que es la Tierra).

Busto de Aristóteles del Palazzo Altemps, copia romana de un original griego del s. IV a. C. [dominio público].

Otras menos pesadas también sienten la misma tendencia natural, pero al ser menos intensa tienden a formar una esfera que rodea a la anterior. Se trata de los líquidos como el agua. En otra esfera concéntrica con ella están las sustancias aún más leves, como los gases y el fuego. Cuando un cuerpo no está en su posición natural, sufre una fuerza –en este caso debida a su gravedad o levedad– que lo lleva a esa posición natural, y en ese momento la fuerza desaparece.

Observa que hablo del lugar natural de las sustancias y no los cuerpos, porque Aristóteles era consciente de que lo importante era lo primero y no lo segundo, incluso a pesar de que no realizase experimentos sistemáticos. No hay más que ver una piedrecilla en un estanque de agua y observar que la piedrecilla –mucho menos pesada que toda el agua del estanque– se hunde hacia el centro de la Tierra y desplaza el agua hacia arriba al moverse.

Dicho de otro modo, un cuerpo tiende a una posición natural más o menos cerca del centro de la Tierra debido a la sustancia de la que está hecho, es decir, a la gravedad específica de esa sustancia. La gravedad específica de la piedra es mayor que la del agua, de modo que cualquier objeto de piedra –da igual su masa total– tendrá una posición natural más cerca del centro de la Tierra que cualquier cosa hecha de agua.

El arquitecto e ingeniero romano Marco Vitruvio Polión, que realizó bastantes más experimentos que Aristóteles, lo explica de un modo cualitativo pero empírico en su tratado De Architectura del siglo I a. C.:

Si se vierte el mercurio en un recipiente, y se deja sobre él una piedra de cien libras, la piedra flota sobre la superficie y no puede hundirse en el líquido, ni romperlo, ni separarlo. Si quitamos la piedra de cien libras y ponemos un escrúpulo de oro [una moneda, la tercera parte de un dracma], no flotará, sino que se hundirá por sí mismo hasta el fondo. Por lo tanto es innegable que la gravedad de una sustancia no depende de la magnitud de su peso, sino de su naturaleza.

Moneda de una libra flotando en mercurio [Alby / Creative Commons Attribution-Sharealike 3.0 License].

Ahora bien, para Aristóteles el peso total del objeto sí importa, aunque no sea para determinar su lugar natural: cuanto más pesado es un cuerpo más rápido será su movimiento hacia el centro, es decir, hacia abajo. Dicho más técnicamente, la velocidad es proporcional al peso del cuerpo. Ya sabes, por la introducción, que esto es falso, y estudiaremos con algo más de detalle la demostración de que lo es, pero no es tremendamente obvio que lo sea, y por eso tardamos siglos en darnos cuenta.

De hecho, desde el siglo XXI es muy fácil esbozar una sonrisa al leer las ideas de Aristóteles, porque en muchas cosas son tremendamente ingenuas; nuestra reacción natural en estos casos es fijarnos en aquello en lo que la idea que leemos está equivocada, y pasar por alto aquellas cosas en las que no sólo no lo está sino que es tremendamente aguda. Permíteme, por lo tanto, que defienda a Aristóteles.

El de Estágira postula la existencia de una fuerza fundamental en la Naturaleza, la gravedad, que tiene que ver con la tendencia de los cuerpos a ser atraídos hacia el centro de la Tierra. Esto significa que, para Aristóteles, no hay un “abajo” como dirección absoluta, sino que se trata de una dirección relativa al centro de la Tierra. Si alguien viajase a las antípodas de Atenas, por ejemplo, y dejase caer una piedra, la gravedad de la piedra la llevaría en sentido opuesto al de una piedra soltada en Atenas.

Esto es de una percepción muy afilada: lo intuitivo es pensar que “abajo” es una dirección absoluta y que quienes viven “abajo” deberían caerse. No sólo eso, sino que este razonamiento lleva al maestro de Alejandro a la conclusión de que, dado que los objetos tienen tendencias de diferente grado a viajar hacia el centro, y dado que no pueden conseguirlo todos los cuerpos, se formarán una serie de esferas concéntricas alrededor del centro, con los materiales más graves cerca y los más leves lejos. Y esto es precisamente lo que sucede, y la razón de que la Tierra tenga la estructura que tiene.

La esfericidad de la Tierra concuerda con la concepción aristotélica de gravedad [NASA]. Versión a 2048x2048 px.

Desde luego, Aristóteles se equivoca en varias cosas: la fuerza no es proporcional a la velocidad, y la velocidad no es proporcional al peso del objeto. Y, sobre todo, la gravedad no es una propiedad de los objetos, sino una interacción entre ellos y la Tierra o lo que quiera que los atrae. Pero darse cuenta de estas cosas –sobre todo de la última– es muy difícil, y el prestigio de Aristóteles hacía aún más difícil cuestionar su concepción de la gravedad.

Ya vimos en la primera parte de la introducción que, sin embargo, pronto hubo quien cuestionó al padre de la Física. De hecho Estratón de Lámpsaco, director del Liceo fundado por el propio Aristóteles, ya puso de manifiesto unas décadas después de la muerte del de Estágira que si se deja caer la misma piedra desde dos alturas diferentes, el agujero que hace en el suelo es mayor cuanto más lo es la altura de caída – pero si la velocidad es uniforme y sólo depende del peso de la piedra, ambos deberían ser exactamente iguales.

Curiosamente era más fácil cuestionar a Aristóteles poco tiempo después de morir que después: su talla fue creciendo en las mentes de los hombres hasta que se convirtió en un gigante casi incuestionable, ni con argumentos ni con experiencias. Como muestra, un botón.

Seguro que recuerdas a Juan Filópono, el filósofo bizantino del siglo VI d. C. que postuló la existencia del ímpetu de los objetos en movimiento. Lo que tal vez no recuerdes es que entonces dije que Filópono había cuestionado otra idea aristotélica más, con un argumento muy sagaz y sorprendente: es hora de hablar de ese argumento.

Filópono hizo algo casi inaudito en su época, un milenio antes de que Galileo Galilei lo convirtiera en un pilar de la Ciencia: realizó experimentos cuantitativos para verificar hipótesis. Y sus conclusiones en cuanto a la gravedad fueron sorprendentes, ya que descartaban las ideas aristotélicas. Filópono pretendía comprobar si realmente la velocidad con la que un cuerpo cae al suelo es proporcional a su peso, de modo que hizo precisamente eso – dejar caer una serie de cuerpos de pesos diferentes y medir los tiempos que tardaban en alcanzar el suelo.

A pesar de que Filópono no era un experimentador tan cuidadoso como Galileo –ya veremos por qué más adelante– y sus experimentos eran más bien burdos, fue capaz de darse cuenta de que Aristóteles no tenía razón. El alejandrino lo dejó absolutamente claro en su discusión sobre la gravedad aristotélica. Antes de leerlo recuerda que estamos hablando del siglo VI d. C. y Aristóteles es casi completamente incuestionable, y date cuenta del énfasis revolucionario de Juan Filópono en la primaciá de la observación frente a la argumentación:

[…] Pero esto es completamente erróneo, y nuestra idea puede ser corroborada completamente por la observación real más eficazmente que por cualquier forma de argumentación verbal. Puesto que, si se dejan caer dos pesos desde la misma altura, uno de ellos muchas veces más pesado que el otro, se comprueba que la proporción entre los tiempos necesarios para completar la caída no depende únicamente de los pesos, sino que la diferencia de tiempos es muy pequeña.

Tan explícito y radical fue el rechazo de Filópono a la idea aristotélica que el pobre fue casi totalmente ignorado en esto: probablemente había intentado ir demasiado lejos y demasiado rápido. Irónicamente, no se había dado cuenta de cuán equivocado estaba Aristóteles: no es que los tiempos sean muy parecidos, es que si se eliminan todos los efectos ajenos a la gravedad los tiempos son completamente iguales. Pero para llegar a ese punto hacía falta una elegancia y meticulosidad en la experimentación para la que hacían falta otros mil años.

Fue entonces cuando la gravedad aristotélica sufrió, no un cuestionamiento como el de Filópono, sino una destrucción total y absoluta, ya que se topó con un genio como ha habido pocos: el pisano Galileo Galilei. El italiano se enfrentó al problema conociendo las pegas que otros antes que él –no sólo Filópono sino muchos otros en el Renacimiento– habían planteado ante Aristóteles.

En una primera etapa Galileo llegó a la conclusión de que Aristóteles estaba en lo cierto en una cosa: la gravedad determinaba la velocidad con la que caen los cuerpos. Ahora bien, el italiano planteó una hipótesis diferente a la del griego: que no es el peso del cuerpo lo que importa, sino el peso específico –la gravedad específica aristotélica– de la sustancia. Es decir, cualquier objeto hecho de plomo caerá a la misma velocidad que otro hecho del mismo material, y un objeto hecho de una sustancia diez veces más ligera caerá diez veces más lentamente.

Galileo Galilei (1564-1642) [dominio público].

Galileo, que era bastante sinvergüenza pero también un genio descomunal, propuso un experimento mental absolutamente demoledor para descartar la conexión aristotélica entre peso de objeto y velocidad de caída. El experimento es el siguiente: imaginemos que tomamos una enorme bola de metal que pesa diez veces más que una segunda bola del mismo metal.

Si dejamos caer la bola mayor y la menor a la vez, de acuerdo con Aristóteles la mayor caerá diez veces más rápido, puesto que pesa diez veces más. Pero hagamos algo diferente: unamos ambas bolas con un cable. La bola mayor cae más rápido, pero la menor más despacio, luego la menor irá retrasándose frente a la mayor y en muy poco tiempo el cable estará tenso y la bola menor estará frenando el movimiento de la mayor. Ambas juntas caerán más despacio que la bola mayor por sí misma.

Pero en la misma física aristotélica esto es absurdo: el conjunto de las dos bolas y el cable pesa más que la bola grande sola, de modo que su velocidad de caída debería ser más rápida juntas que la de la bola grande por sí misma. Aristóteles predice en este caso dos cosas contradictorias y la teoría aristotélica de la gravedad es, por lo tanto, incoherente. Sé que el experimento mental y las conclusiones son discutibles, ¡pero no me negarás que muestran un ingenio colosal!

Estas ideas fueron escritas en un libro, De Motu (Sobre el movimiento), que Galileo empezó a escribir hacia 1589 pero no publicó. Él mismo se dio cuenta de que había cosas que no encajaban, que hacía falta realizar otros experimentos; no estaba suficientemente seguro de que las ideas fuesen correctas y trabajó en el libro durante mucho tiempo. Pero, de hecho, sus ideas finales sobre la gravedad y la caída de los cuerpos fueron publicadas en un libro diferente y eran bastante distintas de las iniciales de De Motu.

El libro en el que el divino pisano plantea sus ideas sobre la gravedad y, de paso, establece las bases de la Ciencia experimental moderna, es una maravilla de la que hemos hablado a menudo y que llevo mucho tiempo traduciendo muy poco a poco –y algún día imagino que publicaremos aquí–: Discorsi e dimostrazioni matematiche, intorno à due nuove scienze (Discursos y demostraciones matemáticas en torno a dos nuevas ciencias), de 1638.

Portada del Discorsi de 1638 [dominio público].

Una de esas dos nuevas ciencias era el estudio del movimiento, es decir, la cinemática, y como parte fundamental de ella Galileo estudia el movimiento de caída de los cuerpos debido a la gravedad. La leyenda, al parecer originada por un biógrafo de Galileo, dice que dejaba caer objetos desde lo alto de la Torre de Pisa. Esto muy probablemente es falso, o si es cierto sólo le sirvió para confirmar aspectos cualitativos, como veremos por la enorme precisión de sus experimentos reales.

Para empezar, Galileo rescata la idea de Estratón y descarta la de Aristóteles (y la suya propia en De motu) de que los objetos caen con una velocidad uniforme: los objetos pesados caen con un movimiento acelerado. Los ligeros también lo hacen, de hecho, hasta que alcanzan una velocidad límite en la que la resistencia del aire les impide seguir acelerando, pero los muy pesados pueden mantener esa aceleración hasta el final.

De hecho, la hipótesis de Galileo es bien simple: de no existir resistencia del aire, la velocidad aumentaría uniforme y constantemente. En los Discorsi el de Pisa lo pone en palabras de su alter ego, Salviati:

Un objeto que cae acelera uniformemente: gana cantidades iguales de velocidad en intervalos de tiempo iguales, de modo que si cae desde el reposo se moverá dos veces más rápido tras dos segundos que como se movía tras un segundo, y tres veces más rápido tras tres segundos que como se movía tras un segundo.

Su problema era que era incapaz de medir esas velocidades y tiempos: los movimientos eran demasiado veloces, y sus instrumentos de medida demasiado imperfectos. De modo que Galileo realizó la serie de experimentos científicos más precisa jamás realizada hasta entonces por el ser humano para determinar si su hipótesis era correcta.

No voy a aburrirte aquí con la descripción minuciosa de la preparación, pero sí quiero resaltar algo: en los Discorsi Galileo describe exactamente la preparación del experimento, los materiales, los tamaños, las formas de medir, etc. De este modo cualquier otra persona que quiera comprobar si su hipótesis es cierta o no puede hacerlo sin el menor problema. Como digo, la ciencia experimental alcanza su madurez con Galileo, y ésa es una de las razones.

Galileo no deja caer objetos en el aire por dos razones: es algo demasiado rápido para medirlo con precisión, y la fricción con el aire perturba los resultados y no permite saber cuál es realmente el efecto de la gravedad en ausencia de otros factores. De modo que se dedica a dejar caer bolas de bronce por rampas.

El de Pisa construye rampas de madera con surcos muy bien pulimentados, los recubre con pergamino y pule bolas de bronce hasta hacerlas lo más suaves y lisas posibles. Puesto que conoce la relación cualitativa de la fricción con el aire y la velocidad, intenta que la velocidad de las bolas no llegue a ser muy grande, de modo que mantiene sus rampas no demasiado inclinadas. Además hace marcas en las rampas que miden exactamente lo mismo, de modo que puede determinar la distancia recorrida por una de las bolas de bronce.

Para medir tiempos, Galileo utiliza una clepsidra, es decir, un reloj de agua. Pero esto tampoco lo hace a ojo: recoge el agua caída por el agujero en un recipiente y luego lo pesa para determinar la cantidad exacta que ha caído. Y tampoco se fía demasiado de esto, ya que repite cada experimento con las mismas condiciones cien veces, para luego obtener datos medios de todas las mediciones.

Réplica de una de las rampas de Galileo [Museo de la ciencia de Florencia].

Y su conclusión es muy clara: todos los objetos, independientemente de su masa y la gravedad específica de sus materiales, aceleran exactamente al mismo ritmo, de modo que su velocidad es proporcional al tiempo que llevan moviéndose desde el reposo y la distancia recorrida es proporcional al cuadrado del tiempo:

Tras haber realizado este proceso y habernos asegurado de su fiabilidad, dejamos caer la bola rodando una cuarta parte de la longitud de la rampa; y habiendo medido el tiempo de su descenso, vimos que era exactamente la mitad del anterior [el experimento anterior comprendía la rampa entera]. A continuación probamos con otras distancias, comparando el tiempo de toda la longitud con la de media, o con la de dos tercios, o tres cuartos, o cualquier otra fracción. En esos experimentos, repetidos un centenar de veces, siempre observamos que los espacios recorridos eran proporcionales a los cuadrados de los tiempos, y esto era cierto para cualquier inclinación de la rampa por la que hicimos rodar la bola.

De modo que, a partir de Galileo, tuvimos claro que la gravedad no hace que los cuerpos se muevan: los acelera. El pisano no definió una magnitud llamada aceleración, de modo que estoy usando términos anacrónicos, pero básicamente llegó a la conclusión de que en caída libre y sin aire cualquier objeto –cualquier objeto, independientemente de lo pesado que sea– se moverá 10 m/s más deprisa cada segundo que el segundo anterior.

Y esto es raro: es intuitivo pensar que los objetos caen más rápido cuanto más pesados son, como así sucede cuando la resistencia del aire es un factor muy relevante. Así, si dejamos caer un martillo y una pluma, evidentemente el martillo llegará al suelo primero, pero de acuerdo con Galileo esto se debe al efecto del aire. De hacer el experimento sin aire, ambos llegarían al suelo a la vez. Ya he mostrado este vídeo hace tiempo, pero no podemos seguir sin verlo como homenaje al pisano, ya que la experiencia, realizada por la misión Apolo 15 en la Luna, se realizó precisamente en honor a Galileo:

Como ves por los experimentos del Galileo, para él lo “natural” –en términos aristotélicos, claro– no es estar parado. De hecho, lo natural para cualquier objeto sometido a la gravedad es moverse cada vez más deprisa si parte del reposo. Pero ¿y si no hubiese gravedad?

Por ejemplo, imaginemos una bola de bronce sobre una de sus rampa acanaladas, pero en este caso colocada de forma horizontal (de modo que no cae hacia ninguna parte), e imaginemos que no hay rozamiento alguno con la rampa ni resistencia del aire. Y supongamos que la bola no parte del reposo, sino que le damos un impulso inicial de 5 m/s. ¿Qué hará entonces de manera “natural”?

De acuerdo con el italiano, lo que hará es seguir moviéndose a 5 m/s, y sé que ya hemos hablado de ello, pero quiero ir más allá de esto, porque Galileo era un genio de verdad. Lo que piensa el de Pisa es lo siguiente: imaginemos ahora que esta rampa horizontal está sobre una mesa, y que la bola se mueve por la rampa a 5 m/s hasta llegar al borde.

¿Qué le pasará a la bola tras abandonar la rampa y quedar en el aire?

Lo magnífico de Galileo en este caso no es tanto la respuesta –que es genial– sino el modo en el que llega a ella, que sigue introduciendo de manera magistral las Matemáticas en la Ciencia. El italiano descompone el movimiento de la bola en dos componentes perpendiculares entre sí.

Por un lado, la bola avanza horizontalmente hacia delante a 5 m/s como hacía antes de manera “natural”. De hecho, el estar sobre la rampa o no no cambia absolutamente nada de este movimiento, ya que lo que hacía la rampa era evitar que la bola cayese, pero no tenía influencia alguna sobre su movimiento horizontal.

Por otro lado, la bola cae verticalmente hacia abajo 10 m/s más rápido cada segundo, como consecuencia de la gravedad. Esta gravedad se dirige exactamente hacia el centro de la Tierra, luego no tiene el menor efecto sobre la velocidad horizontal de la bola.

Es decir, que el objeto tiene un movimiento total que es la suma de dos: uno de ellos horizontal y uniforme, y el otro vertical y acelerado. Galileo llega a la conclusión maravillosa de que esta combinación, en la que un objeto avanza lo mismo cada segundo en una dirección, pero avanza cada vez más rápido en la otra –y con una velocidad proporcional al tiempo– es un movimiento parabólico.

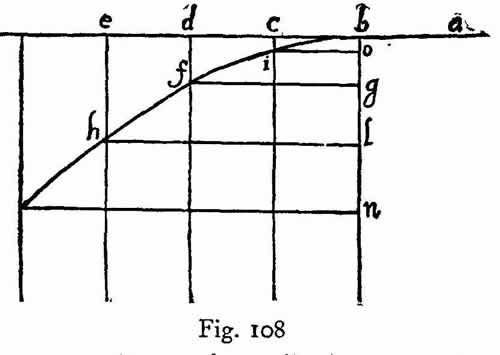
Movimiento parabólico de un proyectil en el aire, de los Discorsi [dominio público].

Su interés no es únicamente teórico, por cierto: el Gran Duque de la Toscana está enormemente interesado en el movimiento de proyectiles en el aire, ya que los cañones son ya un arma importante en la guerra. De hecho Galileo procede luego a estudiar el movimiento con diferentes ángulos de tiro, incluyendo la resistencia del aire y muchas cosas más. Pero esto no es lo relevante para nosotros.

Más allá de la maravillosa geometría y la cuantificación que introduce en la Ciencia, Galileo produce aquí algo aún más interesante por lo que vendrá después: deduce, a partir de un concepto básico –la aceleración del movimiento vertical y la uniformidad del horizontal, a causa de que la gravedad está dirigida hacia abajo–, la forma concreta de una trayectoria. Este poder de predicción es crucial, y lo será muchísimo más cuando lleguemos a Newton, ya que una concepción diferente de gravedad produciría trayectorias diferentes.

El modelo galileano, aunque de una sofisticación barroca frente al de Aristóteles, sigue siendo bastante ingenuo. El centro de la Tierra es el destino de los cuerpos graves, y la gravedad sigue siendo la antigua gravitas, es decir, una propiedad de los cuerpos. Sin embargo, la descripción de Galileo explica maravillosamente bien la caída de los cuerpos y los movimientos de proyectiles en el aire.

Pero entonces surge una aparente contradicción: por un lado los objetos caen hacia el centro de la Tierra debido a la gravedad, es decir, “pesadez”. De hecho, al mezclar sustancias de diferente densidad las más densas –las más graves en términos aristotélicos– descienden al fondo. Luego parece que el peso de los objetos es relevante, como resulta evidente al hacer la experiencia del martillo y la pluma en una habitación con aire.

Pero, por otro, esa misma propiedad que los hace caer es exactamente igual para todos ellos, pluma, martillo o lo que sea. ¿Cómo es esto posible? Si el peso da igual, ¿por qué los objetos pesados quedan en el fondo y tienen una tendencia más intensa a llegar allí que los ligeros? Y si no da igual, ¿por qué todos caen al mismo ritmo?

Y hay otro misterio más. Como sabes de sobra si llevas mucho tiempo con nosotros, Galileo destroza por completo otra idea aristotélica: la noción geocentrista del Universo. Según Aristóteles existe un punto que constituye el centro de todo lo que existe: el punto que atrae a toda la materia pesada, que forma esferas concéntricas según su densidad como hemos visto antes. Ese punto, que es el centro del mundo, es el centro de la Tierra, como no podría ser de otro modo ya que toda esa masa rocosa tiende a apelotonarse alrededor del centro.

Pero, según Galileo, la Tierra no es el centro del Universo ni mucho menos: lo es el Sol. Luego entonces la Tierra no se ha formado alrededor del punto que atrae a todo lo demás, ya que de ser así todo –incluyendo el Sol– giraría en torno a ese punto, y esto no es así. De hecho en el modelo galileano es la Tierra la que gira en torno al Sol realizando órbitas circulares: ¿por qué?

La Luna y la Tierra: un movimiento inexplicable según la gravedad galileana [ESA].

El italiano no responde a esa pregunta.

Galileo sigue sometido, aunque sea un rebelde, a la concepción Aristotélica que separa de manera absoluta el mundo que nos rodea en la Tierra de lo que hay “ahí fuera”. Para comprender el comportamiento de la gravedad hacía falta ir más allá de las balas de cañón galileanas: hacía falta darnos cuenta de que la misma gravedad que hace caer una manzana de un árbol es la que hace que la Luna realice órbitas alrededor de la Tierra.

Otros científicos de la época intentaron explicar el porqué de los movimientos circulares alrededor del Sol y la Tierra. Uno de ellos, aunque equivocadísimo, serviría de inspiración para otros más certeros. Se trataba de William Gilbert, un médico y físico inglés del siglo XVI. En el año 1600 –tres décadas antes de los Discorsi de Galileo– Gilbert publicó un libro sobre el magnetismo, De Magnete, en el que estudiaba esta misteriosa fuerza.

William Gilbert (1544-1603) [dominio público].

Volveremos a Gilbert cuando hablemos de la fuerza electromagnética, pero lo interesante ahora mismo es que Gilbert es consciente de que la Tierra actúa como un imán –una idea correcta–, y dado que la Luna gira alrededor de la Tierra, el inglés deduce que el magnetismo terrestre actúa sobre la Luna a distancia y la mantiene orbitando la Tierra –una idea incorrecta–.

Pero, por más erróneo que sea pensar que el campo magnético terrestre es quien atrapa a la Luna en una órbita a su alrededor, Gilbert ha dado un paso fundamental: tiene la noción de una fuerza que actúa a distancias astronómicas, una influencia de la Tierra sobre la Luna debida a la acción a través del éter –pues casi todos, por entonces, consideran que existe una sustancia que llena el mundo entre los astros–.

Gilbert supondría una gran influencia para otro científico preocupado por el movimiento de los astros y las causas de ese movimiento: el alemán Johannes Kepler. Este matemático, astrónomo y astrólogo sería quien proporcionaría a Isaac Newton –el verdadero padre de la teoría de la gravedad científicamente sólida– el trampolín para crear ese magnífico aparato teórico.

Kepler, a su vez, obtuvo los datos empíricos para deducir sus ideas del danés Tycho Brahe. Kepler trabajó con Brahe durante cierto tiempo, y luego (a la muerte de Brahe en 1601) lo sucedió como astrónomo de la corte del Emperador Fernando II de Habsburgo. Tycho Brahe había amasado una auténtica fortuna de datos astrónomicos detalladísimos, que mantenía en un secreto paranoico –aún no estamos en la época en la que los descubrimientos científicos tienden a compartirse rápidamente–, pero permitió a Kepler utilizar algunos de ellos, y a la muerte de Brahe su sucesor tuvo a su disposición todos los datos de Tycho.

Johannes Kepler (1571-1630) [dominio público].

Con esos datos, que permitían a Kepler conocer la posición de los planetas con una gran precisión a lo largo de décadas, el alemán llegó a conclusiones sorprendentes. El planeta que Tycho había medido con mayor frecuencia y precisión, por realizar un movimiento muy peculiar, era Marte. Lo extraño en el movimiento de Marte es que, visto desde la Tierra, al trazar su trayectoria a lo largo de un año el planeta realiza un movimiento retrógrado de vez en cuando, es decir, cambia su sentido de movimiento aparente alrededor de la Tierra.

La razón es, por supuesto, que Marte no gira alrededor de la Tierra sino alrededor del Sol. Ptolomeo se las había visto canutas para justificar este movimiento retrógrado, y sus modelos del Sistema Solar requerían movimientos circulares dentro de otros movimientos circulares y todo era complicadísimo; con un modelo heliocéntrico, en el que todos los planetas giran alrededor del Sol, el problema desaparecía y quedaba bien explicado el movimiento de Marte. Así, de acuerdo con Copérnico, Marte realiza un movimiento circular uniforme alrededor del Sol.

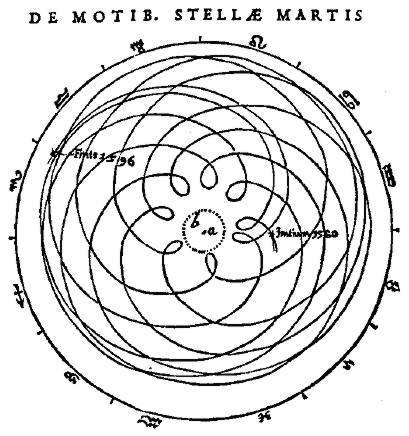
Trayectoria aparente de Marte alrededor de la Tierra, de Astronomia Nova (1609) [dominio público].

Sólo había un problema: cuando Kepler comparaba esa hipótesis con los datos de Tycho de la posición de Marte, no coincidían. La hipótesis del movimiento circular heliocéntrico sí explicaba cualitativamente el movimiento retrógrado de Marte, y si uno no se preocupaba de medir posiciones, tiempos, velocidades y distancias con cierta precisión, todo parecía encajar… pero Kepler disponía de una miríada de datos, y la meticulosidad necesaria para darse cuenta de las diferencias.

El modelo de Copérnico no funcionaba.

No voy aquí a hablar de modelos de Universo durante mucho tiempo, porque lo que nos interesa es la gravedad. En primer lugar, Kepler llegó a la conclusión de que una pequeña modificación al modelo copernicano hacía que los datos empíricos de Tycho se ajustasen como un guante a la teoría: los planetas no giraban realizando circunferencias, sino elipses. Y el Sol no estaba en el centro, sino en uno de los focos de la elipse.

El alemán publicó esta primera ley del movimiento planetario –aún llamada hoy, por razones históricas, primera ley de Kepler–, en un libro de 1609 llamado Astronomia Nova, cuyo nombre ya te da una idea de lo que iba a suponer en unas cuantas décadas. Con la naturaleza elíptica de las órbitas se conseguía adaptar la teoría mucho mejor a la observación; pero había más, y más interesante en cuanto a lo que a la gravedad se refiere.

Kepler se percató de que el movimiento de cada planeta no tenía siempre la misma rapidez. Cuanto más cerca del Sol estaba un planeta, más rápido se movía, y viceversa. Esto lo llevó a enunciar una segunda ley, también publicada en 1609 en Astronomia Nova, en la que afirmó que la línea que une cada planeta con el Sol barre áreas iguales en tiempos iguales.

Es posible que esta animación, que no está a escala con las órbitas planetarias reales –las órbitas de los planetas son casi circulares–, te ayude a verlo:

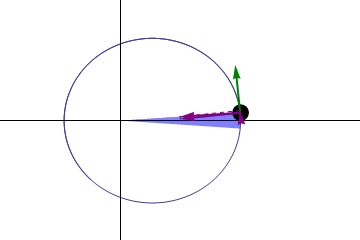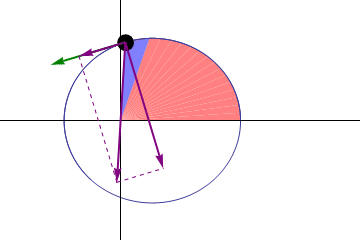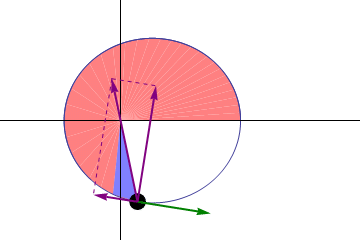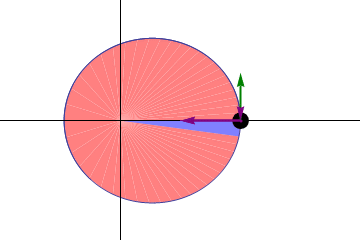
Segunda ley de Kepler [Gonfer / Creative Commons Attribution-Sharealike 3.0 License]

El mérito del alemán está en que no se limitó a decir que los planetas se mueven más deprisa al acercarse al Sol: lo cuantificó, como Galileo en sus experimentos, con una gran precisión. Esto sería absolutamente crucial para que luego Newton hiciera lo que hizo a partir de lo publicado por Galileo y Kepler.

Lo que no consiguió Kepler fue explicar por qué. ¿Por qué cuando un planeta está más lejos del Sol se mueve más despacio, y según se acerca lo hace más deprisa? El mejor intento de Kepler fue a consecuencia de la inspiración de Gilbert. El alemán había leído De Magnete, con lo que no le parecía absurdo pensar en acciones a distancia, pero en este caso no estaba hablando de la Tierra como agente, sino del Sol.

Según Kepler en Astronomia Nova, el Sol es la causa del movimiento en el Sistema Solar. Ese inmenso objeto emite una serie de efluvios que hacen que los cuerpos se muevan.

¿Cómo explica esto la diferencia de velocidad en las órbitas planetarias? Aquí es donde Kepler se lanza al vacío y, sorprendentemente, acierta en algo fundamental: la influencia del Sol disminuye con la distancia.

Así, dado que todo movimiento en el Sistema Solar es a causa del Sol, un objeto muy lejano apenas se moverá, ya que la influencia del Astro Rey es minúscula a esa distancia. Mientras tanto, objetos que pasan muy cerca notarán intensísimamente el “alma solar”, que los impelerá a moverse como locos. Al observar el movimiento elíptico de un planeta somos testigos del cambio: según el planeta se acerca al Sol, siente más los efluvios motrices y acelera, y lo contrario según se aleja del Sol.

Sé que esto tiene incorreciones por todas partes, pero no olvides las dos ideas centrales: el Sol afecta a los otros cuerpos a distancia, pero no a todos por igual, ya que su influencia no es universal e ilimitada, sino que disminuye con la distancia a los objetos. Estas dos ideas serían cruciales para que Newton desarrollase una auténtica teoría universal de la gravitación.

Kepler, además, hace algo que Galileo no hace: intenta encontrar sentido a la contradicción entre la noción aristotélica de gravedad y el abandono del modelo aristotélico –geocéntrico– del Universo. A ver si puedo explicar de dónde sale la contradicción.

Ya vimos cómo, de acuerdo con Aristóteles, la Tierra es una esfera porque toda esa masa tiende a moverse hacia el centro del Universo, que es el centro de la Tierra. Si pensamos, como Copérnico y Galileo, que el Sol es el centro y no la Tierra, ¿por qué la Tierra es entonces esférica? ¡No hay ninguna tendencia natural a que la materia se apelotone de ese modo!

Dicho de otra manera, la gravedad aristotélica es absoluta: se basa en un punto especial, el centro de todas las cosas. Pero ahora ya no hay un absoluto; de acuerdo con Kepler ni siquiera el Sol es el centro de nada, ya que está en un foco de las elipses. ¿Cómo explicar entonces que la materia no se disgregue en los planetas?

La solución de Kepler es, una vez más, consecuencia de leer a Gilbert y De Magnete. En Astronomia Nova el alemán explica lo siguiente, que debes leer recordando que es décadas anterior a Newton. Si te sirve, imagina al inglés leyendo estas mismas líneas, porque sabemos que las leyó como inspiración de su propia teoría gravitatoria:

La gravedad es la tendencia mutua de los cuerpos de la misma naturaleza a unirse unos a otros; así, la Tierra atrae una piedra mucho más que la piedra atrae a la Tierra. La capacidad magnética es otro ejemplo de este tipo […]

Si dos piedras se situasen cerca la una de la otra en algún lugar del mundo lejos de la esfera de influencia de un tercer cuerpo similar, estas piedras, como dos cuerpos magnéticos, se acercarían hasta juntarse en un punto intermedio, y cada una se acercaría a la otra una distancia proporcional a la masa de la otra […]

Se deduce de esto que el poder de atracción de la Tierra probablemente se extenderá hasta la Luna y mucho más allá, y del mismo modo que nada que esté hecho de cualquier forma de material terrestre, por más que se aleje de la Tierra, podrá escapar del alcance de este inmenso poder de atracción.

Creo que no tengo que añadir mucho más. Kepler tomó los modelos copernicanos y, basándose en los datos de Tycho, extrajo conclusiones absolutamente maravillosas, que no restan mérito a Newton, pero ¡qué inteligencia la del alemán, por Dios!

Y es que la cosa no acaba aquí. En la siguiente década, entre 1617 y 1621, Kepler publicó una obra en siete volúmenes, Epitome astronomiae Copernicanae (Epítome de astronomía copernicana), en la que enunció una tercera ley del movimiento planetario –que aún llamamos tercera ley de Kepler–.

Es una ley poco impresionante, pero absolutamente –no, de verdad, absolutamente– crucial para Newton. Básicamente, la tercera ley compara órbitas de distintos planetas, y afirma cualitativamente hablando que cuanto más grande es la órbita, más lentamente se mueve el planeta. Observa la diferencia con la segunda, que hablaba de la variación de velocidad de un mismo planeta en su órbita.

Pero Kepler no es un cualitativo del tres al cuarto, como espero que haya quedado claro. Lo que dice de verdad es lo siguiente: el período orbital de un planeta y la longitud del semieje mayor de la elipse de su órbita están relacionados de modo que el cuadrado el período es proporcional al cubo del semieje mayor.

No dice simplemente que a mayor semieje de la elipse mayor período, ni a mayor semieje menor velocidad, ni nada tan vago como eso: expresa una relación exacta de proporcionalidad con potencias de ambos. Cualquier teoría que intente explicar la gravitación a partir de entonces debe predecir esa extrañísima proporcionalidad.

Impresionante.

Sin embargo, al principio Kepler no impresionó a casi nadie. La reacción de genios de la talla de Galileo ante la publicación de Astronomia Nova fue la más humillante: ni lo mencionaron. De hecho hubo a quien incluso le pareció mal esto de mezclar física y astronomía: intentar emplear la primera para explicar las causas de la segunda era considerado en cierto modo “ensuciar” algo puro y matemático con algo muy inferior.

Pero claro, lo bueno de enunciar leyes con una precisión cuantitativa terrible es que no hay más que hacer una cosa: observar y comprobar si se cumplen sus predicciones. En unos cuantos años, pero desgraciadamente sobre todo tras su muerte, las leyes de Kepler demostraron una solidez apabullante y predijeron multitud de observaciones de los movimientos de los planetas.

El Epitome se convirtió a mediados del XVII en “el” libro de astronomía en las universidades europeas, y nadie se atrevió a cuestionar ya las elipses, las velocidades variables ni la relación período-semieje. Finalmente, Kepler ganó… pero no del todo. La mayor parte de los astrónomos siguieron ignorando sus ideas físicas sobre fuerzas a distancia y demás zarandajas.

Hasta que unos cuantos científicos –casi todos físicos y no astrónomos, pues por entonces los segundos eran matemáticos–, unas décadas más tarde, no sólo demostraron que Kepler tenía razón en mezclar ambas, sino que hicieron de la Astronomía una rama más de la Física; hasta tal punto que uno de ellos, el físico más genial de todos los tiempos, demostró las tres leyes del movimiento planetario de Kepler a partir de leyes físicas más simples, y nos regaló una auténtica teoría de la gravitación.

No hace falta que diga el nombre de ese genio: a su trabajo sobre gravitación dedicaremos el próximo artículo. Espero, querido y paciente lector, que hayas disfrutado de éste, aunque haya sido largo.