Nota: Si ves las fórmulas mal (por ejemplo, si ves símbolos de dólar alrededor de esta $x$) es que no estás leyendo el artículo en la web, que es donde se ve bien. Prueba a leer el artículo original aquí: https://eltamiz.com/2014/05/29/matematicas-i-rectas/.
En la entrada anterior establecimos la base de la geometría analítica en el plano cartesiano. Como espero que recuerdes, terminamos el artículo hablando sobre algunas ecuaciones traducidas al plano, con las soluciones como puntos. Vimos entonces varias ecuaciones que representaban diferentes conjuntos de puntos, sobre todo rectas. Hoy nos centraremos precisamente en ellas, ya que entenderlas lleva a comprender conceptos esenciales para el futuro, como las derivadas y los vectores.
Pero, como siempre, antes de entrar en faena hablemos sobre la solución al desafío anterior.

Solución al desafío 8 - Ecuaciones y puntos
En el desafío se nos pedía encontrar los puntos, conjuntos de puntos o figuras geométricas que resolviesen unos cuantos sistemas de ecuaciones. Vayamos uno por uno.
El primero era el siguiente:
- $x +1 = 0$
- $y -4 = 0$
Se trata de algo que hemos hecho antes varias veces: un sistema de dos ecuaciones con dos incógnitas, y ni siquiera es uno muy difícil. Podemos despejar $x$ e $y$, cada una en su propia ecuación:
$$x = -1$$ $$y = 4$$De modo que hemos encontrado la solución, que es única: el punto (-1,4). Podríamos también haber encontrado la solución llevando ambas ecuaciones al plano cartesiano, ya que tanto una como la otra son sendas rectas, y la solución hubiera sido la misma.
El segundo sistema era un poquito más complicado que el primero, pero no mucho:
- $x = 2$
- $y^2 = 4$
El valor de $x$ ya está ahí, delante de nuestros ojos, y el de $y$ sólo necesita que hagamos una raíz cuadrada:
$$y = \pm 2$$Es decir, en este caso no hay una solución sino dos: $x = 2$, pero hay dos valores posibles de $y$, $y = -2$ e $y = 2$. Los dos puntos del plano correspondientes son (2,-2) y (2,2).
El tercer sistema no tenía mucha chicha de cálculo, pero sí mucha importancia en cuanto a visualizar las cosas en el plano:
- $x + y = 0$
Si recuerdas el artículo sobre sistemas de ecuaciones, en éste hay una sola “pista” pero dos incógnitas. Es un sistema de infintas soluciones, de modo que hay infinitos puntos del plano que la cumplen, pero no todos: (2,2), por ejemplo, no es una solución, ya que $2+2 = 4$, y debe cumplirse $x+y = 0$.
Una manera simple de representar todas las soluciones posibles es despejar una incógnita en función de la otra, por ejemplo, $y = -x$. Por lo tanto, los puntos del plano que resuelven la ecuación son todos aquellos en los que el valor de la abscisa y el de la ordenada son opuestos: (-1,1), (4,-4), (0,0), etc. Dicho de otro modo, son los puntos (x,-x) para cualquier valor de $x$.
En este caso sí puede merecer mucho la pena representar las soluciones en el plano. Si asimilaste bien el anterior sobre las coordenadas cartesianas, seguro que puedes ya ver qué tipo de figura geométrica se formará: es una recta, aunque diferente de las del artículo anterior. Hoy hablaremos precisamente de rectas en general.
Finalmente, el último sistema era el más complicado de todos:
- $x^2 + y^2 = 25$
Una vez más, se trata de un sistema de una ecuación y dos incógnitas, y tiene infinitas soluciones. También una vez más, sin embargo, no todos los puntos del plano son soluciones, ya que (4,4) no cumple la condición, pues $4^2 + 4^2 = 32$, pero la suma de los cuadrados de $x$ e $y$ debe ser 25.
Si despejamos una incógnita en función de la otra, obtenemos algo que tampoco parece muy útil:
$$y = \pm \sqrt{25 - x^2}$$No parece muy obvio lo que es, ¿verdad? Aunque sea difícil ver mucho, podemos al menos obtener algunas soluciones concretas de las infinitas posibles. Así, si hacemos $x = 0$ entonces $y = \pm 5$, con lo que tenemos dos puntos: (0,-5) y (0,5). Lo mismo pasa si hacemos $x = \pm 5$, ya que $y = 0$, con lo que los puntos (-5,0) y (5,0) también son soluciones.
Si recuerdas los cuadrados perfectos hasta el 5 ($5^2 = 25$) podrás obtener también otras ocho soluciones, ya que los únicos números enteros que pueden resolver eso además de los que ya hemos hallado son $\pm 3$ y $\pm 4$, puesto que $(\pm 3)^2 + (\pm 4)^2 = 25$. Los ocho puntos de los que hablo son, por tanto, todas las combinaciones posibles: (-3,-4), (-3,4), (3,-4), (3,4), (-4,-3), (-4,3), (4,-3) y (4,3).
De modo que, aunque haya infinitos puntos que resuelven la ecuación, ya tenemos doce de ellos, y si los dibujas seguramente te harás una idea de por dónde van los tiros:

Aunque puede no ser evidente, y luego hablaremos más en detalle de ello, es una circunferencia. Mi objetivo aquí era que vieses que no es posible únicamente emplear ecuaciones para representar puntos y rectas, sino curvas más complejas, aunque en este bloque no luchemos con ellas.
Rectas en el plano cartesiano
En la entrada anterior vimos algunas rectas en el plano, como $y = 2$ o $x = -2$. La primera era una recta horizontal por encima del eje de abscisas, y la segunda era una recta vertical a la izquierda del eje de ordenadas. Sin embargo, en el desafío hemos visto algo diferente: $x + y = 0$. Si dibujamos unos cuantos puntos verás que se trata también de una recta, aunque no es ni horizontal ni vertical como las anteriores. Basta con representar puntos del tipo (x,-x) que vimos en la solución:
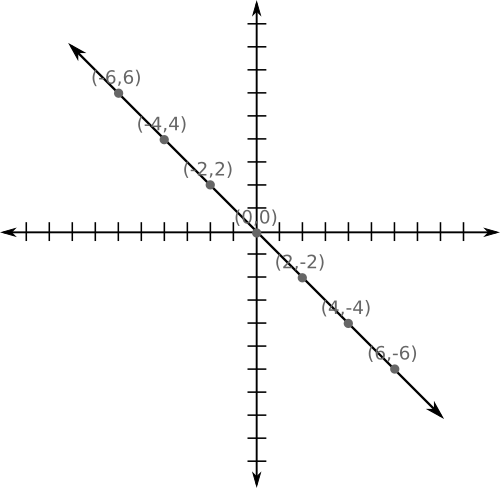
Hoy estudiaremos rectas como esta y otras parecidas: no rectas horizontales y verticales, sino rectas en general. Aunque hay definiciones muy estrictas, y hablaremos más técnicamente de las magnitudes que definen una recta, quiero entrar en el asunto de refilón, para intentar que comprendas la esencia de la cuestión sin apenas darte cuenta. De modo que, si quieres definiciones y fórmulas, por favor, ten paciencia porque llegaremos a ellas – pero, cuando así sea, probablemente ya te dé igual porque hayas comprendido lo que hay debajo.
Como ves en la figura, $x+y = 0$ es la ecuación de una recta oblicua. Esta forma de escribir la ecuación suele denominarse ecuación implícita, lo que significa, dicho mal y pronto, que ambas coordenadas están “mezcladas”, es decir, tratadas por igual en la ecuación y no despejadas una en función de la otra.
Es más común escribir las ecuaciones de rectas, cuando es posible, como ecuaciones explícitas, en las que se ha despejado la ordenada en función de la abscisa. En un momento verás por qué se hace así; la ecuación explícita de nuestra recta oblicua es la siguiente:
Dicho de otro modo, en esta ecuación las dos variables $x$ e $y$ son directamente proporcionales –pero ojo, mira el cuadro de abajo–: duplicar una significa duplicar la otra. Y la constante de proporcionalidad en la ecuación explícita de arriba es -1, ya que conocida $x$ podemos conocer $y$ multiplicando $x$ por -1. Así, si $x = 4$ $y = -4$.
La proporcionalidad es la clave de la existencia de las rectas: lo son porque nunca cambian de dirección. Esto se traduce, en las coordenadas cartesianas, a que cualquier cambio en una de ellas es proporcional al cambio en la otra, y esa proporcionalidad es siempre la misma: es una constante. De no ser así (por ejemplo, si una coordenada es proporcional al cuadrado de la otra), no se trataría de una recta sino de una curva.

¡Ojo! Las variables no son proporcionales, lo son sus cambios
En el ejemplo de y = -x que hemos puesto, las dos variables son proporcionales entre sí. Sin embargo, como veremos luego, esto no siempre es así; hemos empezado con un caso de este tipo porque es la forma más fácil de ver la proporcionalidad que es la base de las rectas.
En general, lo que es proporcional en una recta son los cambios o variaciones de x e y. Dicho de otro modo, si x aumenta en cinco unidades e y lo hace en 10 unidades, entonces segurísimo que si x aumenta en 20 unidades y lo hará en 40.
Esto es cierto, por ejemplo, en y = 2x. Cuando x aumenta en 20, y lo hace en 40 unidades. Pero también es cierto en una ecuación en la que no hay proporcionalidad entre x e y: y = 2x + 10. Si x aumenta en 20 unidades (por ejemplo, de 0 a 20), entonces y lo hace en 40 unidades (de 10 a 50). Las variables x e y no son proporcionales, pero sus variaciones sí lo son.
Esta constante de proporcionalidad se denomina pendiente de la recta. La razón es que, si observamos ahora algunas rectas parecidas pero diferentes, verás que la pendiente determina cómo de inclinada está la recta –es decir, cuánta pendiente tendría si fuese una cuesta arriba o abajo–. Dibujemos estas dos rectas:
Vamos a representar ambas en los mismos ejes para que veas la diferencia entre ambas. Siempre que quieras representar gráficamente cualquier línea, por cierto, recuerda que en WolframAlpha puedes hacerlo simplemente poniendo la ecuación en la caja de texto, si quieres hacerlo mientras lees este artículo. Dicho esto, a veces es conveniente usar un papel y un lápiz y construir la gráfica tú mismo.
En cualquier caso, las soluciones a las dos ecuaciones de antes resultan ser así en el plano cartesiano:

Si empezamos a mirar ambas en el origen, las dos rectas coinciden: (0,0) cumple ambas ecuaciones. No podría ser de otro modo, ya que $x$ e $y$ son directamente proporcionales, luego si una es cero la otra también. Pero, como ves en el dibujo, una de las dos crece mucho más rápido que la otra. En la primera, para que $y$ alcance el valor de 6, $x$ debe ser también 6, pero en la segunda, ya que el valor de $y$ es el doble que el de $x$, basta con que $x = 3$ para que $y = 6$.
Dicho con otras palabras, la segunda recta tiene una constante de proporcionalidad entre x e y que es 2, el doble que la primera. O, mejor aún, la pendiente de la primera recta es 1 y la pendiente de la segunda recta es 2, luego la segunda está más inclinada que la primera. Si pensamos en una recta genérica similar a ellas,
El valor de $a$ determina la inclinación de la recta: de ahí que $a$ sea la pendiente de la recta.
Podrías pensar, por tanto, que un simple número diferencia todas las rectas posibles, pero hay algo más aparte de la inclinación que las diferencia. Así, empecemos con la más simple de las dos anteriores:
¿Cómo podríamos “levantar” esa recta? Dicho de otro modo, ¿no sería posible dibujar otra recta igual que ella, pero que en vez de pasar por el origen de coordenadas lo hiciese por un punto más arriba sobre el eje de ordenadas? Recuerda que la coordenada $x$ indica cuánto a la derecha o izquierda se encuentra un punto, mientras que $y$ indica cuán arriba o abajo.
¿Cómo elevar todos los puntos de una recta tres unidades hacia arriba, entonces? Simplemente sumando 3 a la coordenada $y$. Por lo tanto, partiendo de $y = x$ no tenemos más que hacer $y = x + 3$ y todos los puntos aparecerán tres unidades más arriba que antes. Fíjate, por ejemplo, en el punto (2,2) de la recta original, que ahora es (2,5):

Hemos “levantado” la recta anterior tres unidades hacia arriba. Esto significa que el punto (0,0) de la recta original ahora es (0,3). Dicho de otro modo, la ordenada al pasar sobre el origen es ahora 3. Si hubiésemos construido la recta haciendo $y = x +7$, la recta pasaría 7 unidades sobre el origen de coordenadas (al hacer $x = 0$ obtenemos $y = 7$). Por esta razón este segundo número suele denominarse ordenada en el origen.
Así, nuestra segunda recta $y = x + 3$ tiene de pendiente 1, y de ordenada en el origen 3. El primero nos dice cuán inclinada está –la pendiente 1 significa que $x$ e $y$ aumentan al unísono– y la segunda cuán elevada sobre el origen –el 3 significa que está 3 unidades por encima del origen al pasar por $x = 0$–.
De esta manera, una recta de ecuación $y = ax + b$, da igual cuánto valgan $a$ y $b$, tendrá pendiente $a$ y ordenada en el origen $b$. Por razones que desconozco es común representar estas propiedades con las letras $m$ y $n$, es decir, $y = mx + n$, de modo que intentaré hacer eso aquí.
Espero que veas que modificando estas dos características –pendiente y ordenada en el origen– podemos conseguir absolutamente cualquier recta que se nos pueda ocurrir. Puedes pensarlo así: modificando la pendiente conseguiremos que nuestra recta construida tenga la inclinación de la recta que pretendemos lograr, y una vez hecho eso no tenemos más que modificar la ordenada en el origen hasta desplazar la recta al lugar deseado.

¿Qué pasa con x = 2?
Acabo de decir que cualquier recta puede escribirse básicamente como $y = mx + n$, y que la pendiente y ordenada en el origen determinan la recta, pero ¿cómo se escribe de este modo una recta vertical como algunas de las que vimos en el artículo anterior? Un ejemplo es la recta $x = 2$. ¡En la ecuación ni siquiera aparece $y$! ¿Cuál es su ordenada en el origen, y cuál su pendiente?
Las rectas verticales son un caso algo particular. En primer lugar, dado que la ordenada en el origen es la altura sobre el eje de abscisas a la que pasa la recta sobre el origen, y este tipo de rectas nunca jamás lo hace –con una excepción–, no hay ordenada en el origen. La única recta vertical que sí pasa sobre el origen es el propio eje de ordenadas, cuya ecuación es $x = 0$, pero ¿a qué altura sobre el origen pasa? ¡A todas!
Y ésa es la segunda peculiaridad: la inclinación de una recta vertical es total. No hace falta que $x$ aumente un ápice –de hecho, no puede aumentar si pertenece a la recta– para que $y$ pueda hacerse tan grande o pequeño como queramos. Por lo tanto, la pendiente de las rectas verticales es infinita.
Aunque no hablaremos más de esto en este artículo, recuerda esta caja de texto cuando, cerca del final, te dé una fórmula para calcular la pendiente a partir de un par de puntos de la recta, y verás que esa fórmula obtendría un valor infinito para puntos pertenecientes a una recta vertical.
De modo que simplemente ten en cuenta que esa fórmula genérica es casi universal… pero solo casi, ya que las rectas verticales no pueden describirse con ella.
Por ejemplo, imagina que queremos una recta en la que un cambio en $x$ produce un cambio en $y$ que sea el triple y negativo, es decir, que si $x$ aumenta en dos unidades $y$ disminuya en 6 unidades. Esto significa que la pendiente debe ser -3.
Imagina además que queremos que esta recta no pase por encima, sino por debajo del origen en $x = 0$. Por ejemplo, que pase cuatro unidades por debajo del origen. Entonces, su ordenada en el origen debe ser -4, y puesto que su pendiente es -3, ya tenemos definida la recta:
Pero no hace falta que nuestros requisitos sean tan obvios: básicamente hemos empezado con una pendiente y una ordenada en el origen, pero una recta puede definirse de muchas otras maneras, ¿verdad? Al fin y al cabo es una línea que viene definida por cualquier par de puntos – conocidos esos dos puntos, sólo hay una recta que pase por ellos.
Por ejemplo, si en un dibujo representamos los puntos (-2,4) y (2,2), podríamos tomar una regla y dibujar la recta que pasa por ellos sin el menor problema, aunque no estuviésemos haciendo geometría analítica sino “manual”:
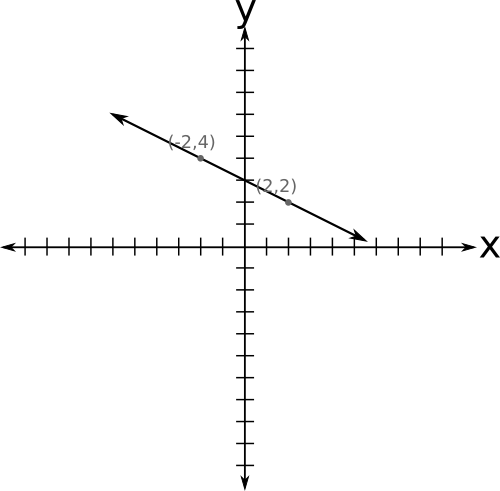
Es posible obtener la ecuación simplemente recordando qué significa, analíticamente hablando, que la recta que deseamos pase por esos dos puntos. Recuerda: todos los puntos por los que pasa la recta deben ser soluciones de la ecuación. ¡Pero si no tenemos la ecuación!, puedes pensar. Partamos, por lo tanto, de una ecuación genérica: $y = mx + n$, donde no conocemos ni $m$ ni $n$, las dos propiedades fundamentales de la recta.
Vamos a darle la vuelta a la tortilla: no conocemos $m$ ni $n$, pero sí conocemos la solución. Por lo tanto vamos a sustituir los valores de $x$ e $y$ que resuelven la ecuación para descubrir cuál es esa ecuación. Hemos dicho que la recta pasa por (-2, 4), lo cual significa que debe cumplirse:
Pero, puesto que la recta también pasa por el punto (2,2),
¿Ves lo que hemos obtenido? ¡Un sistema de dos ecuaciones con dos incógnitas! En vez de ser $x$ e $y$ las incógnitas, lo son $m$ y $n$, es decir, las propiedades de la recta. Resolver el sistema significa, por lo tanto, encontrar la recta que pasa por esos dos puntos.
Si recuerdas los tres métodos básicos de resolución y miras las ecuaciones, verás que en este caso el más eficaz es el de reducción, pues ambas ecuaciones comparten un término opuesto entre ellas. Sumando ambas miembro a miembro,
Luego ya tenemos la ordenada en el origen: $n = 3$. Si te fijas en el dibujo de arriba, en el que simplemente trazamos la recta uniendo los dos puntos con una regla, verás que efectivamente pasa tres unidades por encima del origen. Ahora basta con sustituir $n = 3$ en cualquiera de las dos ecuaciones, por ejemplo la segunda:
De donde $m = -\frac{1}{2}$, luego la ecuación de nuestra misteriosa recta es:
Ya hemos visto lo que significa que $n = 3$, pero ¿qué significa que $m = -\frac{1}{2}$? Es más sutil, pero bastante más importante. En primer lugar, la pendiente de nuestra recta es negativa: esto significa que la recta va descendiendo según nos movemos hacia la derecha. Dicho más técnicamente, cuanto mayor es el valor de $x$ menor lo es el de $y$.
En segundo lugar, el valor absoluto de la pendiente es pequeño: un aumento de $x$ en una unidad supone una disminución de $y$, pero no tanto como aumenta la $x$, sino la mitad. Fijémonos, por ejemplo, en los dos puntos a partir de los que empezamos, (-2,4) y (2,2). ¿Cuál es la diferencia entre ambos en horizontal y vertical?
El segundo punto está 4 unidades a la derecha: 2-(-2). Dado que la pendiente es negativa, está también por debajo, pero ¿cuánto? Tan sólo 2-4 = -2 unidades. Una vez más, la diferencia en vertical es la mitad que en horizontal (-2 comparado con 4, es decir, $-\frac{1}{2}$).
De hecho, esto es lo único necesario para determinar la pendiente de una recta: dividir la variación en $y$ entre dos puntos cualesquiera de la recta entre la variación en $x$. La fórmula matemática puede expresarse así, si los puntos son $(x_1,y_1)$ y $(x_2,y_2)$:
Me he parado tanto con esto de la pendiente porque será fundamental cuando estudiemos, en un bloque superior, el concepto de derivada. Lo importante es que tengas claro que bastan dos números para definir una recta, y qué significa gráficamente cada uno de los dos.
Hay otra idea importante escondida en nuestras rectas, pero para llegar a ella debemos mirarlas de otra manera. Ya hemos visto que es perfectamente posible definir una recta a partir de dos puntos, ya que una recta, por definición, nunca va a cambiar de dirección, de modo que el “rumbo” que lleva del primer punto al segundo es el que llevará siempre.
Esto significa que podemos definir la recta de otro modo: como el “rumbo” que tiene (la dirección de la recta) y un punto por el que pasa. Empecemos por pensar en esto con palabras. Imagina que queremos describir la recta $y = 2$ de este modo, con un punto y una dirección o rumbo. ¿Cómo lo haríamos? Podríamos decir, por ejemplo, que esa recta pasa por el punto (0,2) y es horizontal (dicho de otro modo, su pendiente es 0).
Si se tratase de la recta $y = -2x + 1$ podríamos decir que pasa por el punto (1,-1) y que va hacia abajo y hacia la derecha en un sentido, y hacia arriba y la izquierda en el otro, pero es más inclinada que la diagonal, ya que tiene una pendiente de -2, y la diagonal exacta la tendría de -1.
Pero, como ves, hacer esto con palabras es muy inexacto y farragoso. Es muy fácil identificar un punto cualquiera de la recta, como (1,-1), pero decir hacia dónde va la recta no lo es tanto, con lo que hemos visto hasta ahora. Sin embargo, en Física es absolutamente crucial ser capaz de identificar direcciones de un modo único y conciso, de modo que debemos definir algo que nos sirva precisamente para eso.
“¡Un momento!”, puedes decir. “¡Ya tenemos algo que nos indica la dirección de la recta, la pendiente!” Lo cual es absolutamente cierto. La primera recta que tan torpemente he descrito con palabras pasa por (0,2) y tiene pendiente 0, y la segunda pasa por (1,-1) y tiene pendiente -2. Pero cuantificar una dirección con una pendiente tiene dos problemas:
-
Cuando la dirección es vertical, la pendiente no es un número real, ya que se hace infinita, como hemos visto antes.
-
Cuando abandonemos el plano cartesiano y lleguemos a más de dos dimensiones, el concepto de pendiente se hace mucho menos útil.
Por eso en la siguiente entrada exploraremos, a partir del concepto de recta, uno de los más utilizados en Física: el concepto de vector. Descansa las neuronas hasta entonces… después de terminar el desafío de hoy, of course.
Ideas clave
-
Una recta es el conjunto de puntos solución de una ecuación del tipo $y = mx + n$.
-
La ecuación despejada $y = mx + n$ es la ecuación explícita de la recta.
-
Cualquier otra ecuación en la que no se ha despejado la ordenada, como $ax + by = c$, es una ecuación implícita.
-
En una recta la variación de una de las dos coordenadas es proporcional a la variación de la otra.
-
La constante de proporcionalidad, $m$ en la ecuación explícita, se denomina pendiente.
-
La pendiente de una recta determina su dirección.
-
El término independiente de la ecuación explícita $n$ se denomina ordenada en el origen.
-
La ordenada en el origen indica a qué altura sobre el origen pasa la recta.
-
Una recta está definida única y exclusivamente por dos factores: su dirección (pendiente) y su posición (ordenada en el origen).
-
Es posible definir rectas con otros pares de datos, como por ejemplo dos puntos diferentes, un punto y una dirección, etc.
Antes de seguir…
Puedes imaginarte lo que voy a hacer: pedirte que calcules todo tipo de cosas relacionadas con las rectas. La razón es doble: por un lado, que practiques los sistemas de ecuaciones y las ecuaciones simples. Por otro, que tras trabajar con un puñado de rectas vayas desarrollando la intuición con ellas, de modo que “veas” las cosas sin necesidad de hacer demasiados cálculos en el futuro. ¿Preparado?

Desafío 9 - Rectas y más rectas
Resuelve los siguientes problemas relacionados con rectas, del modo más simple que puedas:
- Encuentra la ecuación de la recta que pasa por los puntos (1,1) y (-4,0).
- Calcula la pendiente y ordenada en el origen de la recta $\frac{y}{4} - \frac{3x}{2} = \frac{1}{2}$.
- Encuentra la ecuación de la recta paralela a $y = -x + 2$ y que pasa por el punto (-2,-2).
- Encuentra el punto de corte de la recta $y = 2x - 5$ con el eje de abscisas y con el eje de ordenadas.
- Las rectas $y = x - 1$ e $y = -2x + 1$ se cortan en un punto. Además, cada una de las dos corta al eje de abscisas en un punto determinado. Estos tres puntos de corte (ambas rectas entre sí y cada una con el eje de abscisas) definen un triángulo. Calcula el perímetro de ese triángulo.
- Encuentra la ecuación de la recta perpendicular a $y = x + 2$ que pasa por el origen.