
Hace ya unos tres meses del último desafío, el de la pendiente infinita. Espero que vuestras neuronas se hayan recuperado y tengáis el lápiz y el cerebro afilados, porque hoy vamos con uno nuevo, el último de este curso escolar.
Si no conoces nuestros desafíos, aquí tienes la presentación y la lista de todos los publicados hasta el momento.
Para quienes aprovecháis estos desafíos para refrescar conceptos vistos en el colegio, hoy os hará falta recordar las poleas. El lugar más eficaz seguramente es el artículo de Wikipedia sobre la máquina de Atwood, ya que como veréis es el núcleo del desafío de hoy.
¿Listos? Vamos con él.
Los koalindres colgantes
La fauna de Wotoda II es peculiar: hay criaturas de veneno tan tóxico que sólo pensar en él mata, carroñeros tan voraces que devoran sus propios cadáveres, plantas herbívoras terroríficas… y los koalindres.
El koalindre es un ser parecido al koala, pero con la capacidad de desdoblarse en dimensiones arbitrarias, tanto las espaciales como la temporal. Así, es posible ver hoy a un koalindre al que uno conocerá mañana, o encontrarse a una manada de cuatro koalindres que ocupan doce árboles, tres árboles cada uno.
Muchos zoos de la Galaxia tienen koalindres: es muy barato, ya que uno o dos de ellos pueden llenar una jaula más bien grande, y es baratísimo mantenerlos. Lo que más les gusta a estas criaturas, aparte de los pistachos, es colgarse de ramas, cuerdas y cosas así. Cuantas más ramas, cuerdas y similares hay en la jaula, más copias de sí mismos hacen los koalindres, ya que les encanta jugar y no quieren dejar ningún juguete vacío.
De modo que, en cierta ocasión, un zoo dirigido por un Alienígena Matemático de gran experiencia decidió hacer un experimento: crear un juego de poleas con cuerdas, de modo que hubiese infinitas poleas, y meter un único koalindre en la jaula. La criatura, con total seguridad, crearía copias de sí misma para colgarse de cada polea… pero, dado que había infinitas poleas, habría infinitos koalindres. Una atracción irresistible para el zoo.
Todo funcionó a la perfección. El koalindre se colgó de la primera cuerda, e inmediatamente realizó copias espaciales de sí mismo para colgar de todas las otras cuerdas, ¡infinitas copias idénticas! La situación inicial era la que se muestra en la figura, con los infinitos koalindres colgando uno de cada cuerda, y cada una de una polea hasta la inicial, colgada del techo:
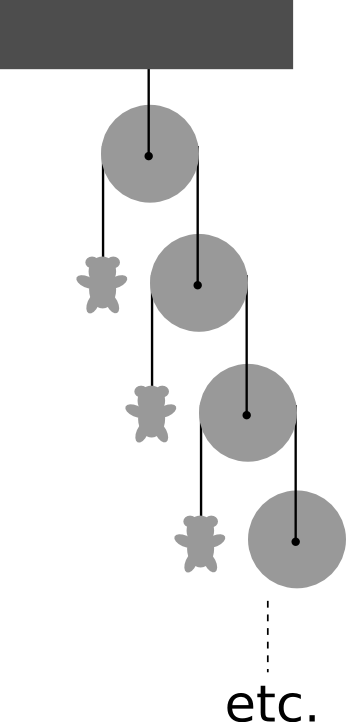
Inicialmente todo el sistema estaba en reposo pero, naturalmente, no estaba en equilibrio, y se puso a acelerar. Y ahí está la pregunta del desafío, que esta vez es sólo una: ¿qué aceleración tiene el primer koalindre? (el más cercano al techo).
Datos para los pejigueros:
-
Todos los koalindres son copias del mismo, luego son todos absolutamente idénticos, con la misma masa M.
-
No hay absolutamente ningún rozamiento, ni en las cuerdas, ni poleas, ni con el aire, ni nada de nada.
-
Todas las poleas son de masa despreciable, lo mismo que las cuerdas, luego cada cuerda tiene la misma tensión en todos sus puntos.
Dejaré los comentarios de esta entrada abiertos por si alguien tiene alguna duda, pero por favor, no deis pistas ni pongáis soluciones aquí. Tenéis hasta el martes 10 de junio para enviar las soluciones a desafios@eltamiz.com. No importa lo pronto que se envíe una solución, sino que sea correcta, que sea clara y esté bien explicada para que puedan entenderla quienes no han podido llegar a la solución buena.
Como siempre, es posible hacerlo en equipo, es posible utilizar programas de ordenador, mejor aún si los ha hecho uno mismo, y lo importante no es llegar a la solución correcta sino disfrutar peleando hasta el final. ¡A por él!